Connection with the SCALe and TARGet keywords

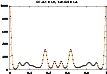
Continuing with the graphical approach, the following diagrams illustrate the effects of using the SCALe and TARGet keywords as if they were adjustable parameters (which they should not).

Figure: SCALe=1.0

Figure: SCALe=0.1

Figure: TARGet=1000

Figure: TARGet=20

Examination of these graphs shows that the effect of SCALe is rather similar to changing the F000. Actually, their effects should be identical, ie giving a SCALe 2.0, F000 50000 should give identical results with SCALE 1.0, F000 25000. The reason for this behaviour is that GraphEnt will NOT apply the scale factor to the F₀₀₀ term.

With the TARGet keyword things are different. The difference of the two maps above (in terms of their sharpness) has nothing to do with scaling or the F₀₀₀ term. The argument in this case is that reducing the target value is to a good approximation equivalent to dividing the standard deviations of your measurements by a constant c > 1.0. In that case, GraphEnt will fit your data closer, meaning that the high resolution data (which usually have the lowest F/(F), will now be reproduced more accurately and will contribute more to your map. Having said that, if the standard deviations were correctly estimated in the first place, you will be fitting noise. Increasing the target value has the opposite effect : GraphEnt will now fit your data less closely, and the GraphEnt map will be more uniform. See page  for an example of using the TARGet keyword in the case of macromolecular anomalous Patterson function calculations.

Take home message : You need data on an absolute scale, with correctly estimated standard deviations. If you have an estimate of a suitable --for your problem-- value for the F₀₀₀ term, use it (edit the MAXENT_AUTO.IN, add a line with the F000 value, re-run with GraphEnt MAXENT_AUTO.IN).