


Next: My native Patterson function
Up: Pathology of GraphEnt calculations,
Previous: The GraphEnt map changes
Contents
All my anomalous Pattersons are ``consistent with a uniform map''
Why : Assume for a minute that all your reflections have the same
F/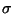 (F) =
(F) = 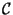 .
Then, because for the
initial (uniform) map all Fourier coefficients are identically zero (with the exception of F000), the statistic
.
Then, because for the
initial (uniform) map all Fourier coefficients are identically zero (with the exception of F000), the statistic
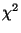 is given by
is given by
where N is the number of observed reflections. Now, the target value for 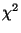 during the calculation is
during the calculation is
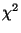 = N. If
= N. If
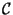 < 1.0, ie
< 1.0, ie
![average[F/sig(F)]](img72.gif) < 1.0,
the uniform map will satisfy the
< 1.0,
the uniform map will satisfy the 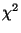 constraint and GraphEnt will stop immediately. Just because GraphEnt stops, does not necessarily mean
that there is no signal in the data : for Gaussian
noise,
constraint and GraphEnt will stop immediately. Just because GraphEnt stops, does not necessarily mean
that there is no signal in the data : for Gaussian
noise,
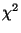
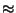 N is the expected value of the distribution
N is the expected value of the distribution
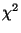
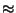 N
N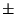
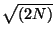 . This means
that depending on the data, the target of the calculation could as well be significantly lower than the value aimed
for by GraphEnt. I think it is worth emphasising this with an example.
The following figure compares the conventional (left) and
GraphEnt (right) map at the section v = 1/2 of the 20-3Å anomalous Patterson function for horse heart myoglobin crystals
(dashed contour at the mean, and then every 0.5 rmsd of the whole map). The
data were collected with CuK
. This means
that depending on the data, the target of the calculation could as well be significantly lower than the value aimed
for by GraphEnt. I think it is worth emphasising this with an example.
The following figure compares the conventional (left) and
GraphEnt (right) map at the section v = 1/2 of the 20-3Å anomalous Patterson function for horse heart myoglobin crystals
(dashed contour at the mean, and then every 0.5 rmsd of the whole map). The
data were collected with CuK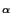 radiation and the anomalous signal comes from the iron atom of heme
(this is one of the examples distributed with GraphEnt, file Myoglobin_anom_Patt_no_outliers.in).
radiation and the anomalous signal comes from the iron atom of heme
(this is one of the examples distributed with GraphEnt, file Myoglobin_anom_Patt_no_outliers.in).
Figure:
Myoglobin anomalous Patterson
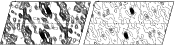 |
A normal run of GraphEnt with the whole data set
would immediately stop with the ``uniformity'' message. Even after rejecting all
reflections with
F/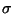 (F) < 0.5, GraphEnt would still refuse to co-operate (for 615 reflections with
F/
(F) < 0.5, GraphEnt would still refuse to co-operate (for 615 reflections with
F/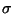 (F) > 0.5, the initial
(F) > 0.5, the initial 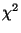 --for the uniform map-- was 502.8). The map shown
above could only be produced after
explicitly setting the TARGet
--for the uniform map-- was 502.8). The map shown
above could only be produced after
explicitly setting the TARGet 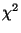 -value to 100.0 (by editing the MAXENT_AUTO.IN file). As you
see, it probably worth the effort20.
-value to 100.0 (by editing the MAXENT_AUTO.IN file). As you
see, it probably worth the effort20.
Getting around it : Start GraphEnt the usual way. When the program stops with the ``uniformity'' message, edit
the MAXENT_AUTO.IN and add a line with a new TARGet value (which should be less than the starting
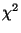 value reported by the program if the VERBose flag is set on, see page
value reported by the program if the VERBose flag is set on, see page ![[*]](cross_ref_motif.gif) ). Depending
on the circumstances, you could also add a line with LIMIt 0.5 to exclude reflections with
F/
). Depending
on the circumstances, you could also add a line with LIMIt 0.5 to exclude reflections with
F/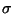 (F) < 0.5
(this should reduce the amount of computation required for convergence).
(F) < 0.5
(this should reduce the amount of computation required for convergence).
Footnotes
- ... effort20
- I should add, however, that I am not convinced that changing the
TARGet
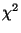 is the correct way around. To continue with the example, even if we take the
expected value of
is the correct way around. To continue with the example, even if we take the
expected value of 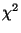 to be
to be
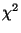
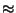 N - 3
N - 3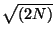 = 509 (ie 3
= 509 (ie 3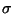 away from the mean),
the uniform map is still consistent with
the data. The fact that there seems to be some signal in the data when we reduce the TARGet, probably points the
way to over-estimated standard deviations.
away from the mean),
the uniform map is still consistent with
the data. The fact that there seems to be some signal in the data when we reduce the TARGet, probably points the
way to over-estimated standard deviations.



Next: My native Patterson function
Up: Pathology of GraphEnt calculations,
Previous: The GraphEnt map changes
Contents
NMG, Nov 2002
![]() (F) =
(F) = ![]() .
Then, because for the
initial (uniform) map all Fourier coefficients are identically zero (with the exception of F000), the statistic
.
Then, because for the
initial (uniform) map all Fourier coefficients are identically zero (with the exception of F000), the statistic
![]() is given by
is given by
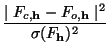 =
= 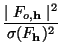 =
= ![]() (F) < 0.5, GraphEnt would still refuse to co-operate (for 615 reflections with
F/
(F) < 0.5, GraphEnt would still refuse to co-operate (for 615 reflections with
F/![]() (F) > 0.5, the initial
(F) > 0.5, the initial ![]() --for the uniform map-- was 502.8). The map shown
above could only be produced after
explicitly setting the TARGet
--for the uniform map-- was 502.8). The map shown
above could only be produced after
explicitly setting the TARGet ![]() -value to 100.0 (by editing the MAXENT_AUTO.IN file). As you
see, it probably worth the effort20.
-value to 100.0 (by editing the MAXENT_AUTO.IN file). As you
see, it probably worth the effort20.
![]() value reported by the program if the VERBose flag is set on, see page
value reported by the program if the VERBose flag is set on, see page ![[*]](cross_ref_motif.gif) ). Depending
on the circumstances, you could also add a line with LIMIt 0.5 to exclude reflections with
F/
). Depending
on the circumstances, you could also add a line with LIMIt 0.5 to exclude reflections with
F/![]() (F) < 0.5
(this should reduce the amount of computation required for convergence).
(F) < 0.5
(this should reduce the amount of computation required for convergence).