The question is : Given a set of incomplete and noisy data
(say,
Fo,![]() with its
with its
![]() (F
(F![]() ) and
) and
![]() ),
which map (of a large number of maps consistent with the observed data)
is the one that will minimise the probability of
misinterpreting it ?
Stating the same problem in a different way, we could ask (i) which map
(of the set of admissible maps) will only show features
for which there is evidence in the data, or, (ii) which map makes the least
assumptions about the data (especially the missing
data, but also the distribution of errors in the observed).
),
which map (of a large number of maps consistent with the observed data)
is the one that will minimise the probability of
misinterpreting it ?
Stating the same problem in a different way, we could ask (i) which map
(of the set of admissible maps) will only show features
for which there is evidence in the data, or, (ii) which map makes the least
assumptions about the data (especially the missing
data, but also the distribution of errors in the observed).
Clearly, the
Fo,![]() exp(i
exp(i![]() ) synthesis is not the map we want :
Not only we assume that all missing data have
F = 0 (a rather improbable event), but also that
F
) synthesis is not the map we want :
Not only we assume that all missing data have
F = 0 (a rather improbable event), but also that
F![]() = Fo,
= Fo,![]() ,
,![]()
![]() .
Gull, S.F. & Daniell, G.J.4, suggested that the map we need is the one for which the
configurational entropy
-
.
Gull, S.F. & Daniell, G.J.4, suggested that the map we need is the one for which the
configurational entropy
- ![]() mjlogmj, where mj is the density
at the grid point j of the map, reaches a maximum. It is easy to see that
-
mjlogmj, where mj is the density
at the grid point j of the map, reaches a maximum. It is easy to see that
- ![]() mjlogmj
reaches a maximum when
mj = e-1,
mjlogmj
reaches a maximum when
mj = e-1,![]() j, that is, when the map has a uniform density, and thus,
contain no information. Maximising
-
j, that is, when the map has a uniform density, and thus,
contain no information. Maximising
- ![]() mjlogmj subject to the constraint that the map
is consistent with the observed data, gives the MAXENT map.
mjlogmj subject to the constraint that the map
is consistent with the observed data, gives the MAXENT map.
The consistency with the observed data is described in terms of the
difference between the observed data and those calculated from a
trial map, weighted by the standard deviation of the measurement.
If
Fc,![]() is the calculated value of the
datum h,
Fo,
is the calculated value of the
datum h,
Fo,![]() its observed value and
its observed value and
![]() (F
(F![]() ) the standard deviation of the observation,
then the statistic
) the standard deviation of the observation,
then the statistic
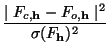
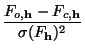 exp(2
exp(2
Given
Fo,![]() ,
,
![]() (F
(F![]() ) and an positive multiplier
) and an positive multiplier ![]() , this equation can determine the
densities m
, this equation can determine the
densities m![]() on a map. The program GraphEnt applies this formula iteratively (starting from a uniform map) until
convergence (as judged by the value of
on a map. The program GraphEnt applies this formula iteratively (starting from a uniform map) until
convergence (as judged by the value of ![]() ) is achieved. Although this algorithm is neither the most efficient nor the most
stable, it is relatively easy to code and it leads (at least in the case of
Patterson functions), to the same results as other, more complex algorithms5.
) is achieved. Although this algorithm is neither the most efficient nor the most
stable, it is relatively easy to code and it leads (at least in the case of
Patterson functions), to the same results as other, more complex algorithms5.