



Next: The slow-cooling mode
Up: Beyond automation
Previous: Beyond automation
Contents
Constant temperature run
In this mode you define a temperature T which
is kept constant for the whole length of the calculation. The maximum
move sizes (how much the parameters that we will test in the next move
may deviate from the current parameters)
are also kept constant for the whole run and equal to :
max( ) = 2dmin/max(a, b, c),
max(
) = 2dmin/max(a, b, c),
max( ) = 2dmin,
where dmin is the minimum Bragg spacing of the input data, a, b, c are the
unit cell translations of the target structure (in Å),
max(
) = 2dmin,
where dmin is the minimum Bragg spacing of the input data, a, b, c are the
unit cell translations of the target structure (in Å),
max( ) is the maximum possible offset for any of the molecular
translations (in fractional units) and
max(
) is the maximum possible offset for any of the molecular
translations (in fractional units) and
max( ) is the maximum possible
offset (in degrees) for
the
) is the maximum possible
offset (in degrees) for
the  angle of any of the molecular orientations18.
angle of any of the molecular orientations18.
The constant temperature protocol can be quite efficient if you know
how to choose a suitable temperature (so that the system is neither thermally disordered, nor
as cold as to get stuck inside a shallow local minimum).
I have recently started trusting the automatic temperature determination performed by QS, and so,
an (automatically determined) constant temperature run is well-worth trying
if the default runs fails to find a convincing solution.
Footnotes
- ... orientations18
-
QS stores the molecular orientations
in terms of the polar angles
 ,
, ,
, .
A new molecular orientation is obtained from the previous one
by rotating the molecule by
.
A new molecular orientation is obtained from the previous one
by rotating the molecule by  degrees about an axis defined by
the
degrees about an axis defined by
the  and
and  angles.
The orientation of the new rotation axis is always chosen randomly in the interval
0
angles.
The orientation of the new rotation axis is always chosen randomly in the interval
0 


 /2 and
0
/2 and
0 
 < 2
< 2 , ie the full half sphere. We
obtain the new orientation by rotating about this axis by
, ie the full half sphere. We
obtain the new orientation by rotating about this axis by
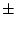
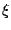
 degrees,
where
degrees,
where
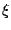 , 0
, 0 
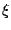
 1 is a random number.
1 is a random number.




Next: The slow-cooling mode
Up: Beyond automation
Previous: Beyond automation
Contents
NMG, January 2005