



Next: Constant temperature run
Up: Qs
Previous: What if automation fails
Contents
Beyond automation
Successive versions of this document contain decreasing amounts of
documentation on the internal workings of the program. The reason for this
inverse relationship is that I can see of no real reason duplicating the
effort that I'm putting in writing the QS-related papers. Electronic
reprints of these papers can be freely downloaded from my homepage and its
mirrors (generously provided by CCP14). The following paragraphs have been
retained because they contain some technical details not available from the
papers.
It is impossible to discuss the input to the program without reference to how the
program works. Table 1 (shown below) outlines the basic steps that QS will follow
under normal circumstances.
The essential ingredients of the reverse Monte Carlo minimisation are (i) that the next
configuration to be tested is chosen randomly, and,
(ii) that the probability of accepting
a move against the gradient (ie. accepting a new configuration although it gives a higher
R-factor) is in general non-zero (so that moves against the gradient are possible).
As is always the case with this type of minimisation algorithms, the
difficult points are : (i) to select the annealing protocol, ie to decide how the
temperature16 varies with respect to time, and, (ii) to
select the displacement vector

 which will take us from the current
configuration
which will take us from the current
configuration  to the new configuration
to the new configuration
 +
+ 
 .
17
.
17
QS supports four different minimisation strategies.
These different annealing protocols are not of cosmetic value : choosing one or the other
might make the difference between solving the structure and wasting CPU time.
Unfortunately, there are no hard and fast rules defining the best minimisation strategy,
and this is one of the basic problems with QS. These three protocols are discussed
in the following sections.
Subsections
- Enter `Queen of Spades''.
- Read in data, coordinates, parameters.
- Translate molecule to 0,0,0, and rotate it so that the axes of inertia are parallel
to the orthogonal frame.
- Generate the electron density map of the rotated/translated molecule in an orthogonal
cell that is at least four times as big as the molecular dimensions.
- Calculate FFT to obtain molecular transform. From now on, to calculate the
contribution of any molecule to any reflection we only have to find the coordinates
of the reflection in the (orthogonal) frame containing the transform and pick-up
the values (real and imaginary) of the transform at that point. No more FFTs, but
interpolation required.
- Assign random orientations and translations to all molecules in the asymmetric unit.
- Calculate and store in memory the
contribution of each molecule in the asymmetric unit (and its
symmetry-related ones) to each reflection. This allows us to make the CPU time per
step independent of the number of molecules (At each step of the minimisation
we only move one molecule,
and, so, the contribution from all other molecules remains the same and we do not
have to re-calculate them). Calculate
initial R-factor, set starting temperature T.
- Begin the basic iteration for a given number of time steps :
- Choose a molecule, a rotation and a translation randomly. Apply the rotation
and translation to the given molecule, and calculate the new R-factor.
- If
Rnew
 Rold, the move is accepted and saved.
Rold, the move is accepted and saved.
- If
Rnew > Rold, the move is accepted with probability
exp(
 R/T), ie. if
exp((Rold - Rnew)/T) >
R/T), ie. if
exp((Rold - Rnew)/T) > 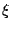 ,
where
,
where 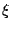 is a random number between 0.0 and 1.0. If that's case, the move
is accepted and saved, otherwise we return to the previous conformation.
is a random number between 0.0 and 1.0. If that's case, the move
is accepted and saved, otherwise we return to the previous conformation.
- The temperature is updated accordingly to a given protocol. The program
supports : (i) a constant temperature simulation, (ii) a slow-cooling
protocol with the current temperature linearly dependent on time,
(iii) a Boltzmann annealing mode, and,
(iv) a variable-temperature heating bath : at regular intervals the program
calculates the average number of moves against the gradient
that have been made in that interval. If this number is less than a preset
value (which may happen when the system is inside a relatively deep local
or global minimum), the temperature is slowly increased until the specified
fraction of moves against the gradient is reached again. This guarantees that
the system will wonder freely from minimum to minimum for the whole run (not
even the global minimum can stop it). This method can only do the job because
at each step the
program examines the R-factor, and if it is the lowest one encountered so
far, it saves the parameters of all molecules.
- Using the parameters that gave the lowest R-factor, calculate orientations and
positions of the molecules and write the .pdb files corresponding to each and every
of the molecules in the asymmetric unit. Generate a .pdb file with all
molecules in the unit cell (to easily check for bad contacts).
- Exit `Queen of Spades''.
Table 1 :
Flow diagram for QS.
Footnotes
- ...
temperature16
- No physical meaning should be attributed to the word `temperature''.
It is only a control parameter which adjusts the probability of accepting a move
against the gradient. The higher the temperature, the higher the probability of accepting
a move that makes the R-factor worse.
- ....
17
- Practically
speaking (and in the case of QS),

 corresponds to the differences
between the current set of orientation angles and positions of the molecules, and the set
that will be tested for the next move.
corresponds to the differences
between the current set of orientation angles and positions of the molecules, and the set
that will be tested for the next move.




Next: Constant temperature run
Up: Qs
Previous: What if automation fails
Contents
NMG, January 2005
![]()
![]() which will take us from the current
configuration
which will take us from the current
configuration ![]() to the new configuration
to the new configuration
![]() +
+ ![]()
![]() .
17
.
17