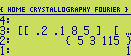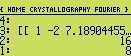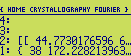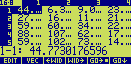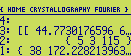Preliminaries
The program Fourier depending on its input will

• Calculate a crystallographic 2D forward Fourier transform (ie., from atomic coordinates to structure factors).
• Calculate a crystallographic 2D inverse Fourier transform (ie., from structure factors to an electron density map).
• Calculate and plot a contour-line representation of a 2D electron density map.

Limitations
The program uses the geometric structure factors equations in plane group p1 to perform the transformations and not a FFT. This has several consequences :

1. The programs are plane-group general but you will have to enter all atoms in the unit cell and all reflections within the full-half circle (note that Friendel's law is being applied internally by the program).
2. The program is slow, especially the inverse Fourier transformation. On my HP48SX, the time requirements for the inverse FT is to a good approximation [GRID_x*GRID_y*REFL*0.1170 seconds] (almost 2.5 minutes for a 16x16 grid and 5 reflections).
3. There are no limitations on the grid size (19 is as good as 16).
4. The code is short : the whole program occupies 2203.5 bytes (checksum 41282d).

The calculator must be in degrees mode and all angles are used and produced as if in degrees mode.

The contouring routine has limited capabilities and will only perform well when the sampling of unit cell is equal (or better) than : 4*max(h) along x, 4*max(k) along y.
Note well : The program only performs rudimentary validity checks on user input. It shouldn't be too difficult to crash the calculator by entering random combinations of numbers and objects through the input lists and arrays.


Using the program
Fourier will read its input from the stack, and will return its output to the stack. Here is a worked example of using the program : We want to calculate structure factors for a p1 structure. Start by creating a [n*4] array holding (x,y,Z,B) where (x,y) are the fractional coordinates of the n atoms, Z are their atomic numbers, and B the temperature factors :


Enter this array on the stack (possibly after saving it to a variable), followed by a list containing unit cell dimensions {a,b,theta}, and finally, the resolution (Bragg spacing) to which you want to calculate structure factors. The stack (before running the program) should look like this :


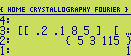
The program will now calculate all structure factors (h,k,|F|,phi) (for the given cell and atoms), lying within the full-half circle corresponding a resolution of 1 Angstroem (if the cell dimensions were given in Angstroem). The result will be a [n*4] array (on level 1) containing the list of structure factors in the form (h,k,|F|,phi) with the angles measured in degrees :


We can now use these structure factors to perform an inverse Fourier transformation in order to calculate an electron density map. Just use the array together with two reals giving the grid spacing along x and y and re-run the program :


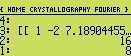
The result will be an array holding the electron density map (on level 2), and a list (on level 1) as shown below :


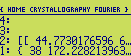
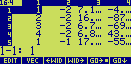
If you edit the list you should see something like this :


The first number is the mean density of the electron density map, the second is the maximum density, and the third corresponds to half of the rms deviation of the densities. The last number is a scale factor used by the program for preparing (subsequently) a contour-line plot of the map. It is the number of pixels (10 by default) per unit length of the cell dimensions (eg. 10 pixels per Angstroem, if the cell dimensions are in Angstroem). If you edit the array on level 2, it should look similar to this :


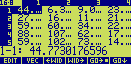
The x axis is vertical, the y is horizontal, and the element (1,1) is the value of the electron density [arbitrary units] at the origin of the unit cell (x=0.0, y=0.0). The map encompasses a complete unit cell without the additional lines of values at x=1.0 and y=1.0 (which belong to neighbouring unit cells). We can now calculate a contour line plot of this electron density map. All that we need is to add a list containing the unit cell dimensions between the array and the list with map parameters :


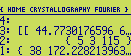
The program will clear the LCD, draw the unit cell and start going through the contour lines. When it finishes (and if the plot was larger than one screen) you can move around the map using the cursor keys. Exit by pressing the ATTN key (this will leave a graphics object on level 1 containing the plot). Note that what you see in a complete unit cell, this time including the additional lines at x=1.0 and y=1.0 (these are generated internally by the program).


The first contour-line is drawn at a density equal to the first number contained in the map parameters list (mean density by default). All other contour lines are drawn with a step equal to the third number in the map parameters list (0.50 of the rmsd by default), until a value equal to the second number is reached (maximum map density by default).
Finally, you can calculate the Patterson function corresponding to a set of structure factors. All you have to do is to re-run the inverse FT but this time give a negative value for one (or both) of the grid definitions (eg. -16 8 or 16 -8 for the example shown above). The output from the program will be a Patterson density map together with its map statistics. Plotting it should give you a familiar pattern :



Nicholas M Glykos, glykos@mbg.duth.gr, http://www.mbg.duth.gr/~glykos/